Harmonic Math

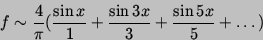
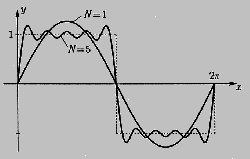
While most sciences created by the man, grow copying imperfectly (mostly), to the nature, the math grow availing the human intellect, with abstractions, inductions, deductions, axioms, analogies, hypothesis and final demonstrations. The math, -with their many variant- are able been prided to be one of the few abstract sciences, created by the humans, with not always visible applications or, utilitarism. A branch of math - the geometry, including their figures: circles, rectángles, triangles, etc- were created by the Greeks. The triangles, were extensively employees by them, to calculate heights of buildings (knowing previously two-sided triangle lengths), eclipses shadows extension, distances of the Earth to the Sun, etc. The abstraction of the Greeks was such that permitted them, to establish relations between arcs and radios (sinus), complementary sinus of angles (cosines), sinus and cosines of angles, etc. Later, when Maxwell studied and explained the laws of electromagnetism, sinus and cosines were indispensable, to decipher the particularities of the electromagnetic waves. Neither that to say of the math applied to the study of the movements of light waves and/or electrons, when the structure of the atom was discovered. At present in Physics, the Unified Theory, intends to explain any natural phenomenon, by means of the Superstrings Theory (waves in last instance).

Since 1966, the swedish Lennart Carleson employing many of the previous concepts -especially the series of Jean Baptiste Joseph Fourier (that relate by means of polynomial and integral formulae, sinus and cosines), isolated in thousands of parts, the compact of waves trapped in the sound of a trumpet or in the sound waves emitted by a violin (harmonic math), concluding that every continuous function -waves in this case- are equal to the sum of their series –parts- of Fourier: The single add of sinus and cosines, permitted in this way to simplify many complex phenomena. Later Carleson noticed that the fluctuations of any metereológic phenomenon, peaks of certain illnesses (epidemics), ascents and descents of values of the market, etc., could simulate waves. Then he tried to predict future events (theory of continuous dynamic systems), obtaining impressive results. Although for the time being the theory is successful to predict future events of natural phenomena of periodic nature, we sense that with certain aggregates (a previous lot of know how, emergency of outsiders, retreat of candidacies, effects of dirty wars, etc), these math, quick will be applied to the presidential electoral processes, permitting to predict with approximations very close to the reality, the final electoral results. Because of it, the 23/05/06, the Norway Academy of Sciences and Letters, will deliver to Carleson, the Prize Abel 2006 of Math –the most important of the world. Good for Carleson.

Matemática armónica.

Mientras que la mayoría de las ciencias creadas por el hombre, crecen copiando imperfectamente (mayormente), a la naturaleza, las matemáticas lo hacen valiéndose del intelecto humano, con abstracciones, inducciones, deducciones, axiomas, analogías, hipótesis y demostraciones finales. Las matemáticas, -con sus variantes- pueden preciarse de ser una de las pocas ciencias abstractas, creadas por los humanos, con aplicaciones no siempre visibles o, utilitarias. Una rama de ellas, la geometría –incluidas sus figuras :circulos, rectángulos, triángulos, etc., fueron creadas por los griegos. Los triángulos, fueron extensamente empleados por ellos, para calcular alturas de edificios (conociendo previamente longitudes de dos lados), extensión de sombras de eclipses, distancias de la Tierra al Sol, etc. La abstracción de los griegos fué tal que les permitió, establecer relaciones entre arcos y radios (senos), senos complementarios de ángulos (cosenos), senos y cosenos de ángulos, etc. Más tarde, cuando Maxwell estudió y explicó las leyes del electromagnetismo, senos y cosenos fueron imprescindibles, para desentrañar las particularidades de las ondas electromagnéticas. Ni que decir de las matemáticas aplicadas al estudio de los movimientos de las ondas luminosas y/o electrones, cuando se descubrió la estructura del átomo. Actualmente en Fisica, la Teoria Unificada, pretende explicar cualquier fenómeno natural, mediante la Teoria de las Supercuerdas (ondas en última instancia).

Desde 1966, el sueco Lennart Carleson empleando muchos de los conceptos anteriores -en especial las series de Jean Baptiste Joseph Fourier (que relacionan mediante polinomios y fórmulas integrales, senos y cosenos), aisló en miles de partes, al compacto de ondas atrapadas en el sonido de una trompeta o en las ondas sonoras emitidas por un violin (matemáticas armónicas), concluyendo que toda función continua -ondas en este caso- equivalen a la suma de sus series –partes- de Fourier : suma de senos y cosenos, casi en todas sus partes, permitiendo simplificar muchos fenómenos complejos. Mas tarde, al percatarse que las fluctuaciones de muchos fenómenos metereológicos, picos de ciertas enfermedades (epidemias), ascensos y descensos de valores de la bolsa, etc., podian simular ondas, teorizó tratando de predecir eventos futuros (teoria de los sistemas dinámicos continuos), obteniendo resultados impresionantes. Aunque de momento la teoria es exitosa para predecir eventos futuros de fenómenos naturales de naturaleza periódica, nosotros intuimos que con ciertos agregados (mucho know how previo, emergencia de outsiders, retiro de candidaturas, efectos de guerras sucias, etc), estas matemáticas, pronto serán aplicadas a los procesos electorales presidenciales, permitiendo predecir con aproximaciones muy cercanas a la realidad, los resultados electorales finales. Por ello, el 23/05/06, la Academia Noruega de Ciencias y Letras, le entregará a Carleson, el Premio Abel 2006 de Matemáticas –el más importante del mundo. Bien por él.